基本原理：

KMP算法是核心是运用双指针算法和递归思想来解决寻找一目标链在模板链中的起始匹配位置，暴力算法便是两指针分别从模板链和目标链的起点开始匹配，看是否相同，如果相同，则两指针同时向右边移动，再继续比较，如果遇到不同，则模板链上的指针要回退到第二个字符位置（即看第二个位置是否能够作为起点来匹配目标链），而目标链上的指针必须回到起点，很明显，这种做法时间复杂度很高，为O(m*n)，而KMP算法就是为了优化朴素算法，将时间复杂度降为O(n+m),KMP算法也是利用双指针算法，但是与朴素算法不同的是，它利用之前上一步已经匹配好的目标链与自身开始匹配不成功的点的前面一段，然后目标链上的指针只需回退到与主链后面已经匹配了的最长位置的后一个字符开始，而主链上的指针不需要移动，只需一直向前移动，目标链上的指针则需要回退和前进，既然需要找主链上从起点到某一位置与模板链上不匹配位置往前的并且可以匹配的最长一段，反正目标链与不匹配链字符前面的一段已经匹配，那么何不直接看目标链已经匹配了的一段，也就是目标链的子链从后看匹配的一段，如果目标链的每一段子链都已经预处理好了，可以以O(1)的时间找到前缀链与后缀链匹配的最长位置，那么目标链上的指针回退到该位置后，便可继续与模板链继续匹配，这便是KMP算法的核心思想。

实现过程：

1、KMP算法核心一步便是对目标链的预处理过程，也就是找到目标链子上的每一段的真前后缀链，next函数的实现

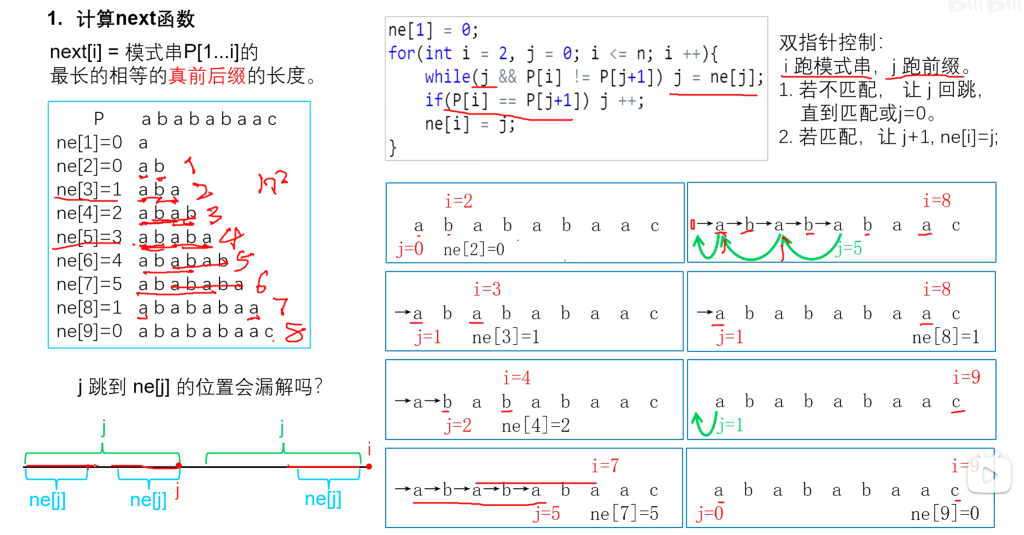
void next(char str[])
{
     ne[1]=0;
     for(int i=2,j=0;i<=n;i++)
     {
          while(j&&str[j+1]!=str[i]) j=ne[j];
     }
     if(str[i]==str[j+1]) j++;
     ne[i]=j;
}

2、目标链与模板链的匹配过程，思路与next函数的实现基本一致

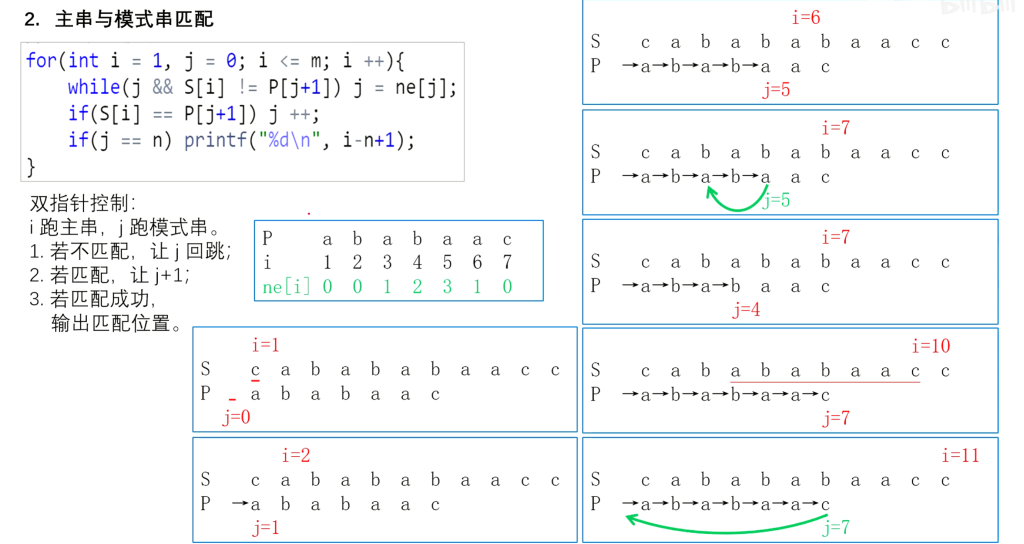
代码实现

for(int i=1,j=0;i<=m;i++)
{
    while(j&&a[i]!=b[j+1]) j=ne[j];
    if(a[i]==b[j+1])
        j++;
    if(j==n) printf("%d/n",i-n+1);
}

例题：

#include <iostream>
using namespace std;
const int N=100010,const int M=1000010;
int n,m;
int ne[N];
char s[M],p[N];
int main()
{
    cin>>n>>P+1>>m>>s+1;
    for(int i=2,j=0;i<=n;i++)
    {
        while(j&&p[j+1]!=p[i]) j=ne[j];
        if(p[j+1]==p[i]) j++;
        ne[i]=j;
    }
    for(int i=1,j=0;i<=m;i++)
    {
        while(j&&s[i]!=p[j+1]) j=ne[j];
        if(s[i]==p[j+1]) j++;
        if(j==n)
        {
            printf("%d ",i-n);
            j=ne
        }
    }
    return 0;
}